Lie ring
In mathematics a Lie ring is a structure related to Lie algebras that can arise as a generalisation of Lie algebras, or through the study of the lower central series of groups.
Formal definition
A Lie ring is defined as a nonassociative ring with multiplication that is anticommutative and satisfies the Jacobi identity. More specifically we can define a Lie ring  to be an abelian group with an operation
to be an abelian group with an operation ![[\cdot,\cdot]](/2012-wikipedia_en_all_nopic_01_2012/I/3587c5df5edf1176ed7afc1f20f5d8a9.png) that has the following properties:
that has the following properties:
- Bilinearity:
- for all x, y, z ∈ L.
- The Jacobi identity:
- for all x, y, z in L.
- For all x in L.
Examples
- Any Lie algebra over a general ring instead of a field is an example of a Lie ring. Lie rings are not Lie groups under addition, despite the name.
- Any associative ring can be made into a Lie ring by defining a bracket operator
![[x,y] = xy - yx](/2012-wikipedia_en_all_nopic_01_2012/I/2d4099ee292ebfa424a594a8233f6a38.png) .
.
- For an example of a Lie ring arising from the study of groups, let
 be a group with
be a group with 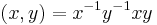 the commutator operation, and let
the commutator operation, and let 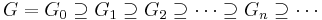 be a central series in
be a central series in  — that is the commutator subgroup
— that is the commutator subgroup 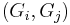 is contained in
is contained in 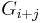 for any
for any 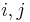 . Then
. Then
- is a Lie ring with addition supplied by the group operation (which will be commutative in each homogeneous part), and the bracket operation given by
- extended linearly. Note that the centrality of the series ensures the commutator
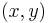 gives the bracket operation the appropriate Lie theoretic properties.
gives the bracket operation the appropriate Lie theoretic properties.
![[x %2B y, z] = [x, z] %2B [y, z], \quad [z, x %2B y] = [z, x] %2B [z, y]](/2012-wikipedia_en_all_nopic_01_2012/I/612225aa111eef27437e38b56c4eb4b3.png)
![[x,[y,z]] %2B [y,[z,x]] %2B [z,[x,y]] = 0 \quad](/2012-wikipedia_en_all_nopic_01_2012/I/69ee53d21fe7eb5e7b8ed7938cb8cab0.png)
![[x,x]=0 \quad](/2012-wikipedia_en_all_nopic_01_2012/I/4b3d4565edeb5d1f29e91ea7b7e4655b.png)
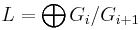
![[xG_i, yG_j] = (x,y)G_{i%2Bj}\](/2012-wikipedia_en_all_nopic_01_2012/I/149ffe3c2874fe451d7f153e86879eb4.png)